 |
| One whole or two? |
3/4 + 5/7 = ?
If you are student who "knows what you are doing" then your work may look something like this:
Since 3/4 = 21/28 and 5/7 = 20/28 then 21/28 + 20/28 = 41/28 = 1 & 13/28
Could the answer ever be: 3/4 + 5/7 = 8/11? "Of course, not," was my gut reaction. But then I read Keith Devlin's* description of how a student can justify this "obviously" wrong answer.
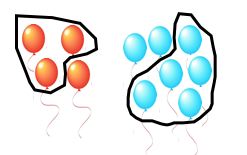
"If I have 4 red balloons of which 1 is burst, than three quarters of my red balloons are good. If I have seven blue balloons and 2 of them are burst, than 5/7 of my blue balloons are good. So what fraction of my balloons are good? Well, altogether I have 4 + 7 = 11 balloons, and of them three are burst, leaving 8 good ones, so the fraction of my balloons that are good is 8/11."Devlin continues:
"This is perfectly correct reasoning, showing that the student understands the concept of fractions. The students problem is that he or she is unaware that, for very good reasons, the mathematical community long-ago decided that adding fractions mean something different from adding proportions even though fractions may be and are used to quantify proportions."Note how the "whole" changes from the first context to the next. So as the saying goes: Keep your eye not on the doughnut, but on the whole when doing fractions.
*Devlin, Keith. "Mathematics Education for a New Era Video Games as a Medium for Learning" p. 68.




No comments:
Post a Comment